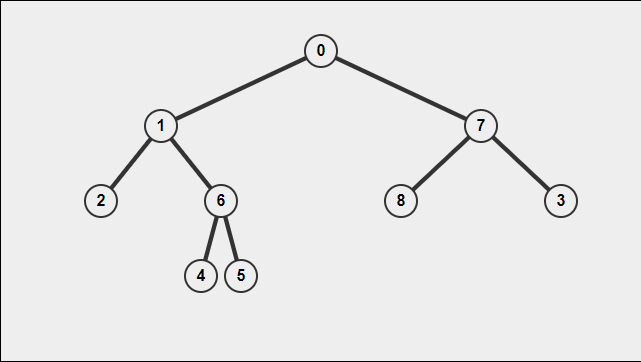
Traversing binary trees is a fundamental skill required for coding interviews. Today I will teach you the main ways of traversing a binary tree. Each traversal style is associated with a specific pattern. Below is a quick reference. (All code examples are worked in python)
Binary Tree Traversal Cheat Sheet
| Traversal | -> | Pattern |
|---|---|---|
| In-order | left/center/right | |
| pre-order | center/left/right | |
| post-order | left/right/center | |
| level-order | left to right |
Example
Pre-Order Traversal
A preorder traversal follows the center-left-right pattern. For the tree above, the output would be [0,1,2,6,4,5,7,8,3]
Solution
def preOrderHelper(tree, array = []):
if tree != None:
array.append(tree.value)
preOrderHelper(tree.left,array)
preOrderHelper(tree.right,array)
return array
In-Order Traversal
An inorder traversal follows the left-center-right pattern. The algorithm will traverse as far left as possible and then add each center node with the right node being added last. An in-order traversal of the graph above would output [2,1,4,6,5,0,7,8,3]
Solution
def inOrder(tree, array = []):
if tree != None:
inOrderHelper(tree.left,array)
array.append(tree.value)
inOrderHelper(tree.right,array)
return array
Post-Order Traversal
A postorder traversal follows the left-right-center pattern. For the tree above the output would be [2,4,5,6,1,8,3,7,0].
Solution
def postOrder(tree, array = []):
if tree != None:
postOrderHelper(tree.left,array)
postOrderHelper(tree.right,array)
array.append(tree.value)
Level Order Traversal
A level order traversal will return a two dimensional list of every level in the tree. For the example above, the result would be:
[[0], [1,7], [2,6,8,3], [4,5]]
The code below uses a helper function. The helper function keeps track of which level of the tree it is located in.
Solution
def levelOrder(root: TreeNode) -> List[List[int]]:
if root == None:
return [[]]
acc = [[]]
helper(root,acc,0)
return acc
def helper(root,acc,ind):
if root == None:
return acc
else:
if len(acc) < ind + 1:
acc.append([])
acc[ind].append(root.val)
helper(root.left,acc,ind + 1)
helper(root.right,acc,ind + 1)
return acc